注冊暖通工程師基礎考試高等數(shù)學知識點(18)
兩平面的夾角
1. 兩平面的夾角: 兩平面的法線向量的夾角(通常指銳角).
設平面П1和П2的法線向量依次為:
n1=(A1,B1,C1) n2=(A2,B2,C2)
則平面П1和П2的夾角θ為(n1^n2)和π-(n1^n2)中的銳角,
Þ cosθ=|cos(n1^n2)|,
即有:
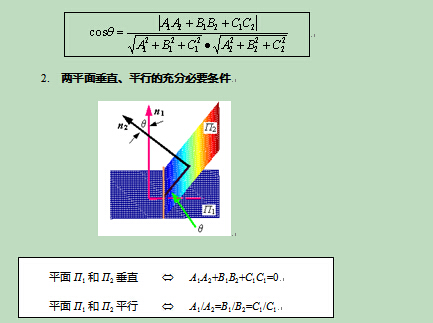
|
平面П1和П2垂直 Û A1A2+B1B2+C1C1=0 平面П1和П2平行 Û A1/A2=B1/B2=C1/C1 |
例1. 求兩平面x-y+2z-6=0和2x+y+z-5=0的夾角.
解: n1=(1,-1,2) n2=(2,1,1)
Þ cosθ= =
Þ θ=π/3
例2. 一平面通過兩點M1(1,1,1)和M2(0,1,-1)且垂直于平面x+y+z=0,求它的方程.
解:設所求平面的一個法向量為 n={A,B,C}.
由n⊥M1M2=(-1,0,-2) Þ -A-2C=0
由n⊥(1,1,1) Þ A+B+C=0
Þ A=-2C,B=C,
代入點法式方程: A(x-1)+B(y-1)+C(z-1)=0
消去C得所求方程為:
2x-y-z=0
點到平面的距離
例3.設P0(x0,y0,z0)是平面Ax+By+Cz+D=0外一點,求P0到這平面的距離.
解:在平面上任取一點P1(x1,y1,z1),并作一法向量n={A,B,C}.
則所求距離:d=│PrjnP1P0│.
又設en為與n方向一致的單位向量,
則有: PrjnP1P0= P1P0•en

